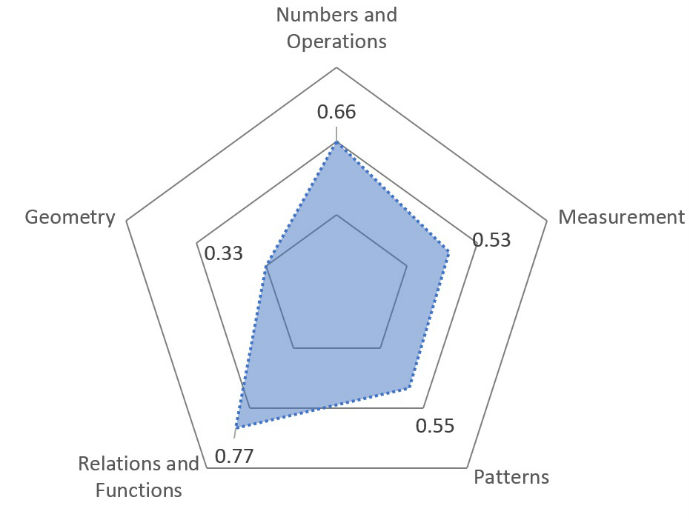
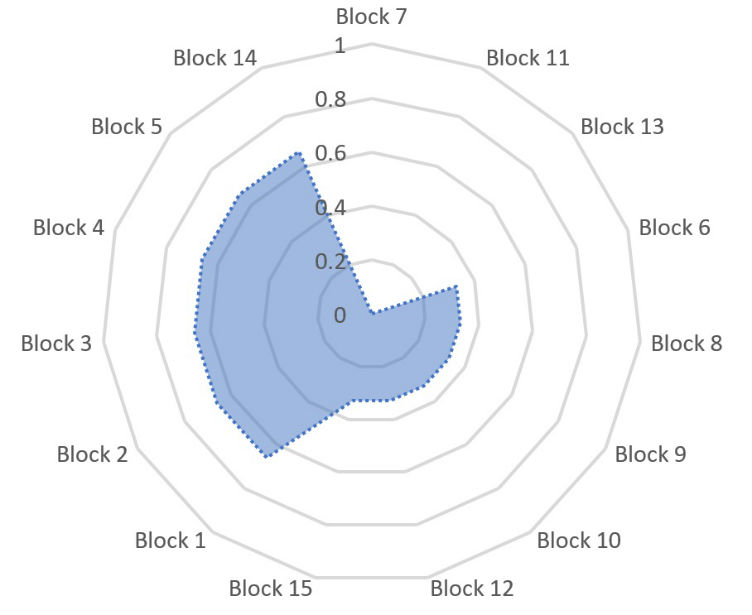
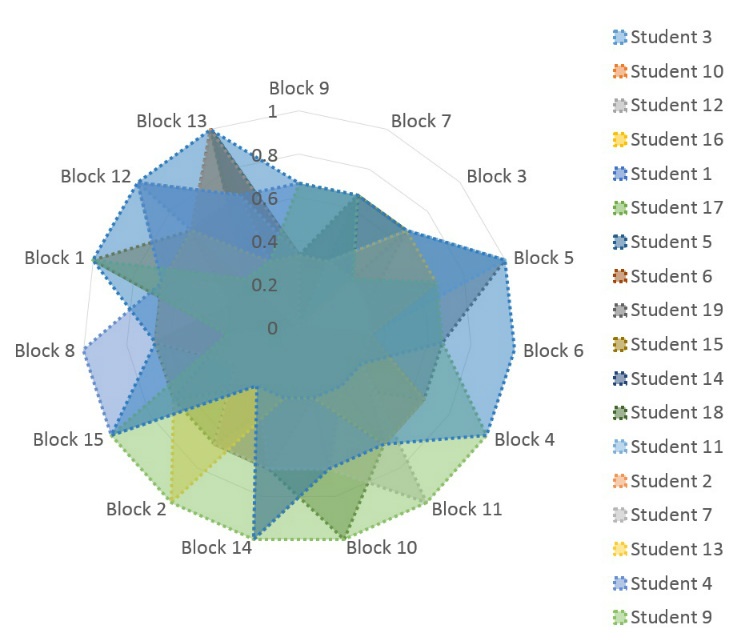
- Development of matrix of main chapters of school subject with summary of educational goals that should be achieved
- Identification of set of tools which acquisition is a foundation related to this chapter
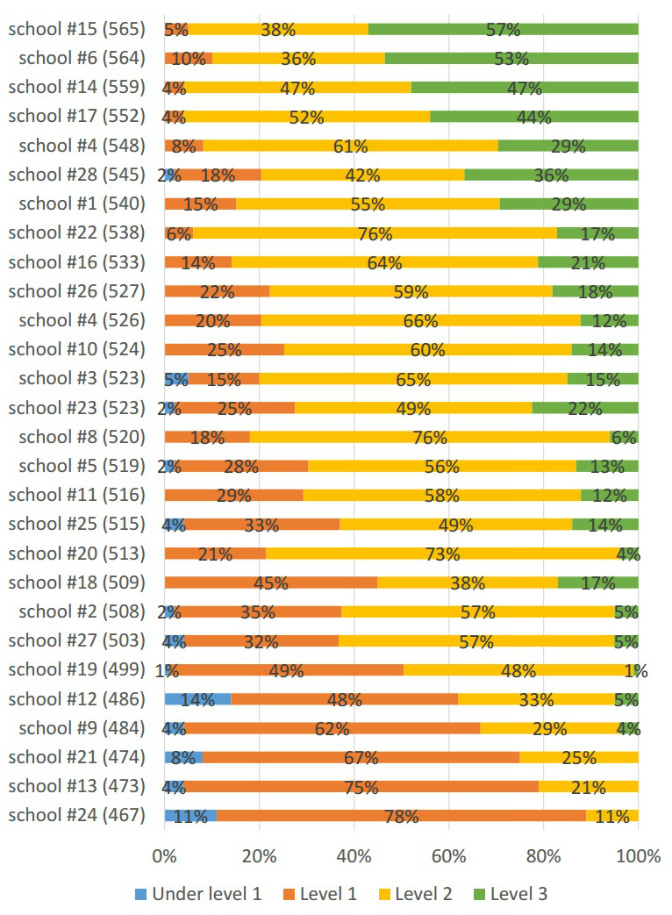
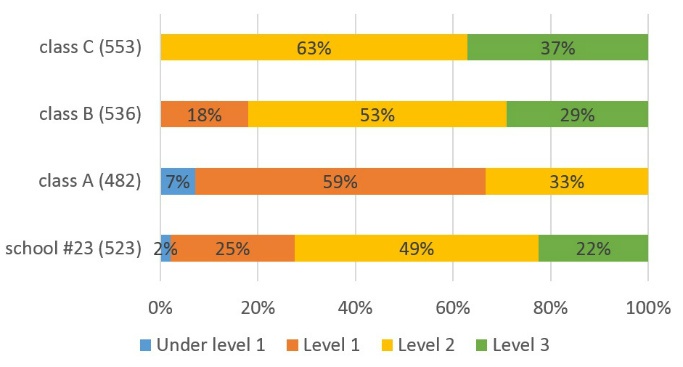
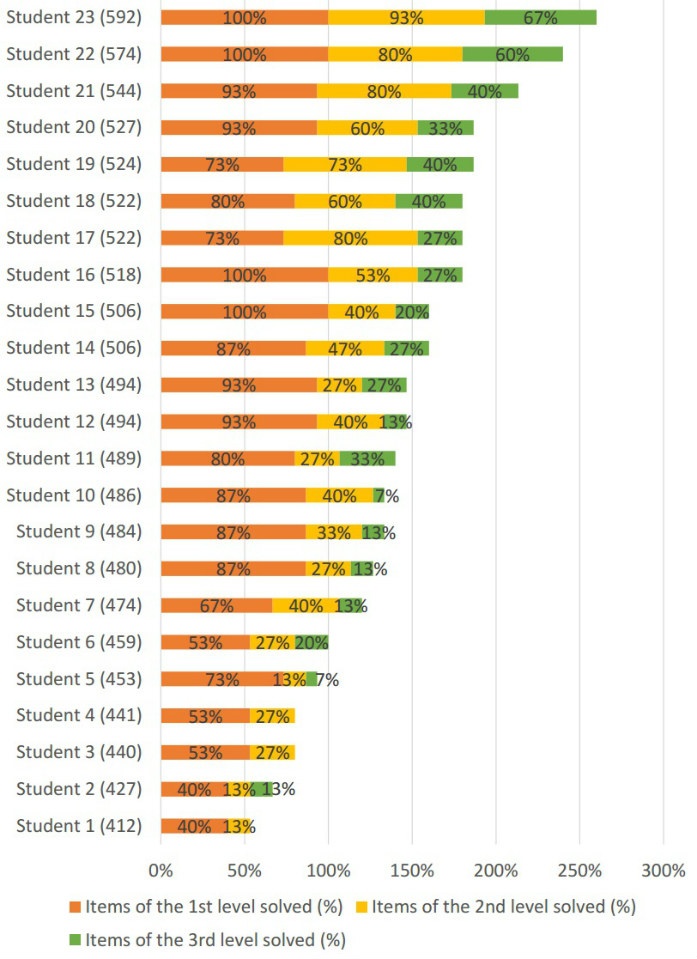
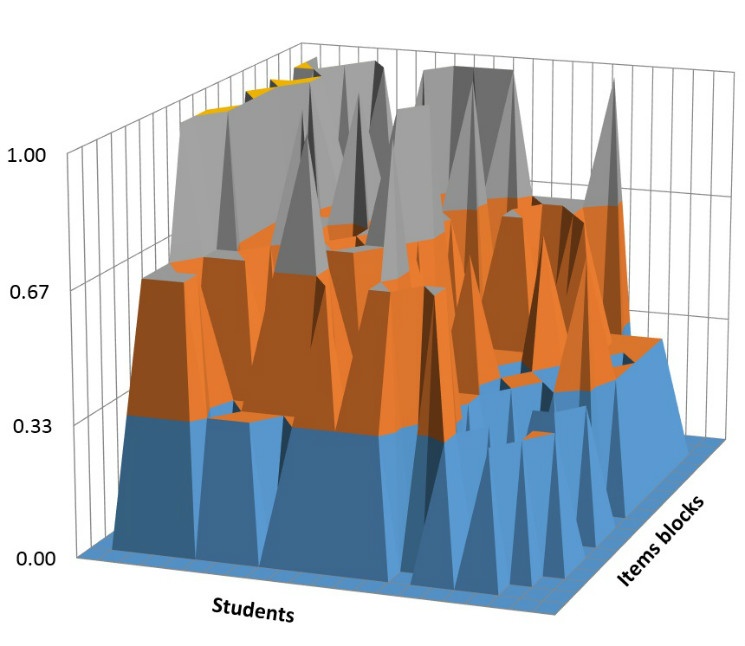
- For each chapter a few blocks of items should be developed. Each of the blocks has items of 1st, 2nd, 3rd level
- Within the block items should form hierarchy by level of difficulty, item of the 1st level is the most simple, item of third level is the most difficult.
Due to such design each block functions as a detector that determines level of knowledge acquisition.
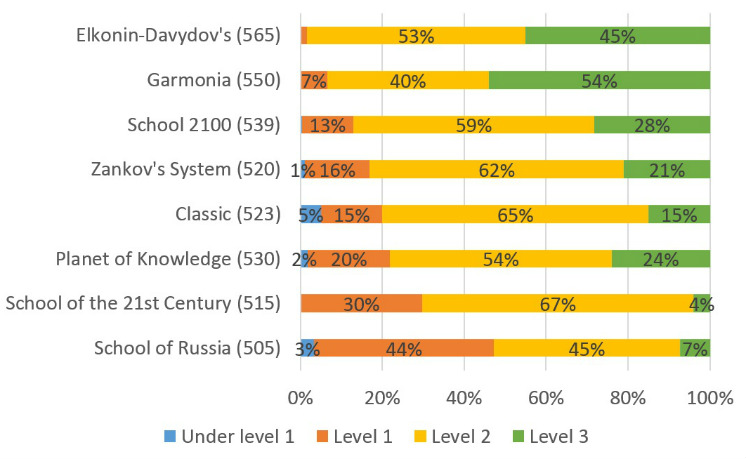
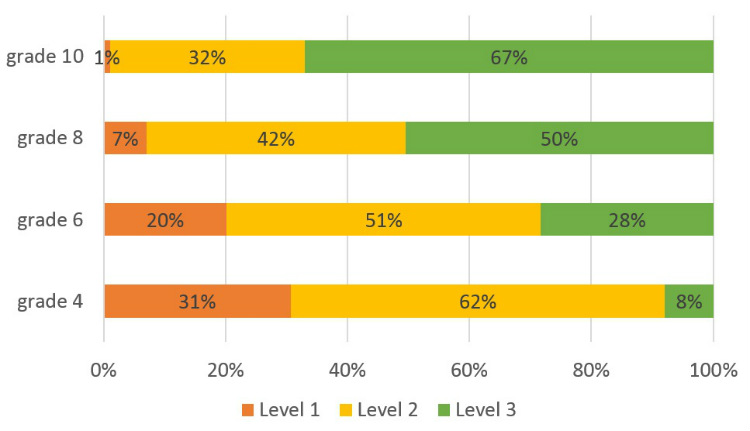
Three levels of items corresponds to three levels of knowledge acquisition
First level (procedural knowledge)
Student orientates towards external (descriptive) features of the problem. It allows to identify it as belonging to a particular category and to invoke an algorithm used for this category of problems. In this case, the description of a problem can be associatively linked to a learned procedure. The formulation of the problem contains direct clues about the required operation, namely division. The problem is presented in a standard way that should be familiar to a student who has learned the corresponding topic. The student still has to know how the algorithm works and some students, especially at the early stages of learning, may find it challenging to follow the steps of the procedure. However, once the procedure is mastered, there is no need to discover new ways of applying this knowledge outside of a standard context.
Second level (conceptual understanding)
Solving problems at this stage generally requires understanding a principle, or a fundamental relation underlying a particular concept. The problems of this level are often formulated in a way that makes it difficult to map their description onto a given algorithm. The student needs to analyze the meaning of the problem, which may require transforming its description in order to understand how to approach its solution.
Third level (functional competence)
Students must develop the depth of understanding and conceptual flexibility that will allow them to see a full range of possiblemental “moves” within the problem space and identify the sequence of moves that leads to a solution. At level 3 it necessarily requires that the child compares multiple ways of approaching the problem. In a way, the child should carry out a series of mental experiments and compare their results.